281
Bearbeitungen
Änderungen
Abkürzung
[[File:Noto Emoji Oreo 26cf.svg|150px|right]]'''Proof of Work''' (Abkürzung: '''PoW''') ist ein verbreitetes Verfahren für einen [[Konsensalgorithmus]], dessen Merkmale ein Arbeitsnachweis sowie Asymmetrie sind. Dabei nehmen am Verfahren zwei Entitäten teil (im Folgenden [[Alice und Bob]]). Alice und Bob haben sich auf einen Proof of Work-Algorithmus geeignet. Gemäß diesem führt Alice mittelschwere Berechnungen durch, die Bob mit geringem Aufwand nachprüfen kann. Das Ausführen dieses Verfahrens im Zusammenhang mit der [[Blockchain]] wird auch als '''Mining''' bzw. '''Schürfen''' bezeichnet.
== Vereinfachtes Beispiel ==
[[File:PrimeDecompositionExample.svg|thumb|Primfaktorzerlegung am Beispiel 864]]
Ein vereinfachtes Beispiel für eine solche Berechnung wäre eine Primfaktorzerlegung: die Zahl <math>424242</math> benötigt zur Faktorisierung mit einem in Python implementierten Algorithmus<ref>Algorithmensammlung: Zahlentheorie: Primfaktorisierung. (1. Juni 2018). Wikibooks, Die freie Bibliothek. Abgerufen am 15. November 2019, 10:51 von https://de.wikibooks.org/w/index.php?title=Algorithmensammlung:_Zahlentheorie:_Primfaktorisierung&oldid=852431.</ref> ca. 80 Schritte (und deutlich mehr CPU-Zyklen), um auf das Ergebnis <math>2 \cdot 3 \cdot 3 \cdot 7 \cdot 13 \cdot 37</math> zu kommen. Für Bob ist der Zerlegung vergleichsweise einfach zu überprüfen: er muss die Zahlen einfach nur wieder zusammenmultiplizieren und schauen, ob wieder die Ausgangszahl herauskommt.<ref group="Anm">Hier wird der Einfachheit halber vernachlässigt, dass Bob überprüfen müsste, ob die Faktoren auch wirklich prim sind, was zuungunsten der Laufzeit geht, sofern auf kein Time-Memory Tradeoff zurückgegriffen wird.</ref> Bei der Zahl 42424242 wären es für Alice bereits ~220 Schritte, bei 4242424242 über 1000.
== Anwendung in der Blockchain ==
# Von jedem Block lässt sich ein Hash erzeugen.
# Jeder Block ist genau dann gültig, wenn er eine festgelegte Aufgabe erfüllen kann.
# Es wird der Zweig der Blockchain verwendet, der valide ist und den größten Arbeitsaufwand benötigte.
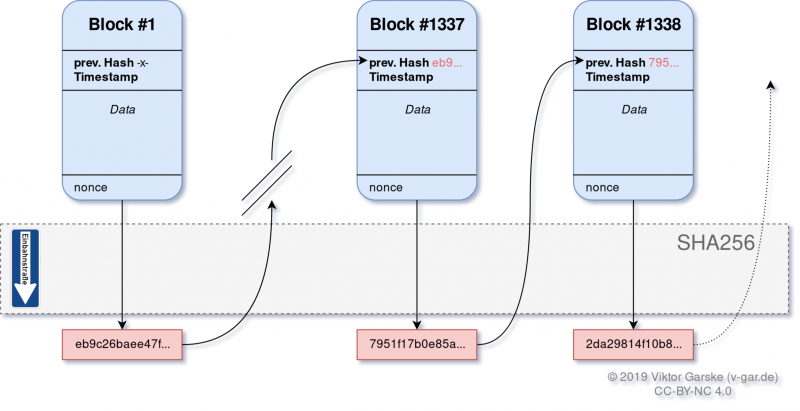
Schematisch sieht das Verfahren so aus:
Hier liegt der Kern des Proof of Works. Damit ein Block als gültig angesehen werden kann, muss eine mittelschwere (aber trotzdem lösbare) Aufgabe gelöst werden. Bei Bitcoin muss z.B. der Hash am Anfang eine bestimmte Anzahl an Nullen haben. Dies ist schwer, weil der Hashalgorithmus für Diffusion (Lawineneffekt) und Konfusion (Einbahnstraße) ausgelegt ist: es muss also solange etwas an der Hashfunktioneneingabe geändert werden, bis ein Hash mit führenden Nullen herauskommt und die Aufgabe somit gelöst ist.
Aber an welcher Stelle können wir jetzt noch was am Block ändern, damit wir den Eingabewert variieren können? Hier kommt der Nonce ins Spiel, dessen einzige Aufgabe in diesem Zusammenhang genau diese die Funktion als variabler Wert zum Verändern der Hashfunktioneingabe ist.
<syntaxhighlight lang="python">
=== Punkt 4: Verfizierbarkeit ===
[[File:Blockchain.svg|thumb|150px|Eine Blockchain. Alle schwarzen Blöcke gehören zu dem Zweig / Branch / Strang, der für die Knoten verbindlich ist.]]
Anhand der im Block abgespeicherten Nonce kann nun die Aufgabe nun von anderen Teilnehmern nachgestellt werden und somit verifziert werden. Schafft man das Ist dies rekursiv bis zum [[Genesis-Block]], dem ersten Block (der keinen weiteren prev_hash hat), möglich, ist der Branch / Zweig valide.
Hat man nun konkurrierende Blöcke, kann mit Rücksicht auf die difficulty Difficulty ermittelt werden, welcher die größte Difficulty hat den größten Aufwand hatte und somit nun verwendet wird.
Beispiel: eine Blockchain hat die Difficulty 10 für alle Blöcke<ref group="Anm">In der Praxis verändert sich die Difficulty von Zeit zu Zeit.</ref>. Es liegen nun zwei konkurrierende Blöcke vor: ein schwarzer und ein lilafarbener Block (siehe Grafik rechts, gemeint sind die Blöcke ersten schwarzen resp. lilalen Blöcke von oben aus gesehen). Mit der Annahme, dass die Ketten für sich valide sind, kann nun die Anzahl der validaten Blöcke der jeweiligen Kette ermittelt werden. Bei Schwarz sind das 9, bei Lila 8. Multipliziert mit der Schwierigkeit 10 sind das für Schwarz 90 und für Lila 80. Der gültige Zweig ist nun der schwarze, da er mit dem höheren Aufwand erstellt wurde.